Magical polyhedra

Flat surfaces were tremendously important to M.C. Escher. A two-dimensional blank sheet of paper gave him the opportunity to explore the infinite and to conjure illusions. On such sheets he would create deceptive three-dimensional worlds in which order and chaos are in conflict, just like in the real world. But despite order frequently losing out to chaos in the real world, Escher turned this on its head. At the awards ceremony for the 1965 Hilversum Culture Prize he had the following to say about it:

‘In my prints I try to convince people that we live in a neat, ordered world rather than in a chaos devoid of standards, as sometimes seems to be the case.’

He often used regular polyhedra – the so-called Platonic and Archimedean solids – to symbolise that order. Two books served as significant sources of inspiration: Algemene mineralogie en kristallografie (1935) by his half-brother Berend, and Vielecke und Vielflache: Theorie und Geschichte (1900) by Max Brückner (1860-1934)*. The latter proved particularly interesting because it featured numerous images, as well as 146 photographs of paper polyhedron models from Brückner’s collection. Escher used these images as sources for his own drawings and models.

The Platonic solids comprise five types of regular polyhedra first described by the Ancient Greek philosopher Plato (427-347 BC): the tetrahedron, the hexahedron (or cube), the octahedron, the dodecahedron and the icosahedron. The Ancient Greek mathematician Archimedes (287-212 BC) subsequently described the thirteen Archimedean solids – semiregular polyhedra which are variants on the Platonic solids. Escher presents several of these polyhedra in his prints, in some instances in modified form. A side view of a cube with three adjoining facets cropped up in Metamorphosis I and Cycle. Reptiles features a dodecahedron. In Crystal he presents us with a combination of cube and octahedron. And in Contrast (Order and Chaos) and Gravity he uses a star dodecahedron – a dodecahedron featuring a five-cornered pyramid on each surface. In Four Regular Solids he even combines four of these polyhedra: hexahedron, octahedron, dodecahedron and icosahedron. He wanted to throw in a tetrahedron for good measure, but eventually decided not to as this would make things overly complex for the viewer **.

Although he had a serious passion for the two-dimensional in his prints, he occasionally switched to creating a real three-dimensional shape. This was sometimes because he wanted to depict such a mathematical solid in a print and needed a model to be able to get it right. It could also be an autonomous solid that could be regarded as a standalone work of art.

For example, he designed a can in the form of an icosahedron for can manufacturer Verblifa. Verblifa produced 7,000 of these cans in 1963. A decade prior to this Escher himself produced two perspex star dodecahedra. It was a thorough production process, which Escher carried out in 1953 in collaboration with his son George, who was studying at the Technical College of Delft. Keen to perfect the first specimen, Escher went for a second attempt. He etched into the individual pieces of perspex a pattern that gives the impression of being a starfish. George was tasked with gluing together all the parts by hand. This project must have been a veritable puzzle for father and son.

The perspex star dodecahedron is currently on display at Escher in The Palace. It is on loan from a private collection and this is the first time that it can be admired in a museum.

Escher wrote about his print Four Regular Solids ***:

‘If you were to ask me why I indulge in such crazy projects, why I create such absolute objectivities that have been stripped of anything personal, then the only answer I could muster would be that I feel compelled to do so. To my knowledge at least, the issue was never satisfactorily resolved by that group of people comprising Dürer, Pacioli, Barbarbo and even Leonardo around 1500 and 1600. I’ve no doubt that they originally found the matter interesting in the same way as I do: the beauty and order of regular solids is overwhelming […]’

Long tradition

There is a long history of regular, semiregular and self-crossing polyhedra in art and science. The Ancient Greek mathematician Euclid (c. 325 BC – 256 BC) was the first person to describe in his treatise Elements the regular shapes defined by Plato. Physical dodecahedra are known to have existed from as early as the Roman era, though their function has never been explained. Polyhedra not only embody elegance and mathematical precision, but are also richly symbolic. Which makes them interesting to both scientists and artists, who have studied the solids and published on them or incorporated them into their art over the centuries. The most famous example is Leonardo da Vinci (1452-1519), the Renaissance artist who stood at the intersection of art and science and with whom Escher felt a tremendous affinity. Da Vinci drew the illustrations of regular polyhedra that featured in the first part of Divina proportione (1509) by Luca Pacioli (1445-1517). In turn, Escher would go on to depict the polyhedra in a similar openwork manner in his print Stars.

Their fascination with these polyhedra allowed Da Vinci and Pacioli to rub shoulders with artist-scientists such as Piero della Francesca (c. 1415-1492) and Albrecht Dürer (1471-1528). They all had to stay on the right side of religion, however, as it was commonplace for scientists to also be clergymen. The Church was a powerful patron and occasionally opponent too. One of the earliest examples of patronage is the small star dodecahedron found in a floor mosaic (c. 1425) in St. Mark’s Basilica in Venice. The mosaic is attributed to Paolo Uccello (1397-1475). Star-shaped polyhedra symbolising God and the Church featured on obelisks and church buildings in Europe during the late Renaissance and subsequent centuries.

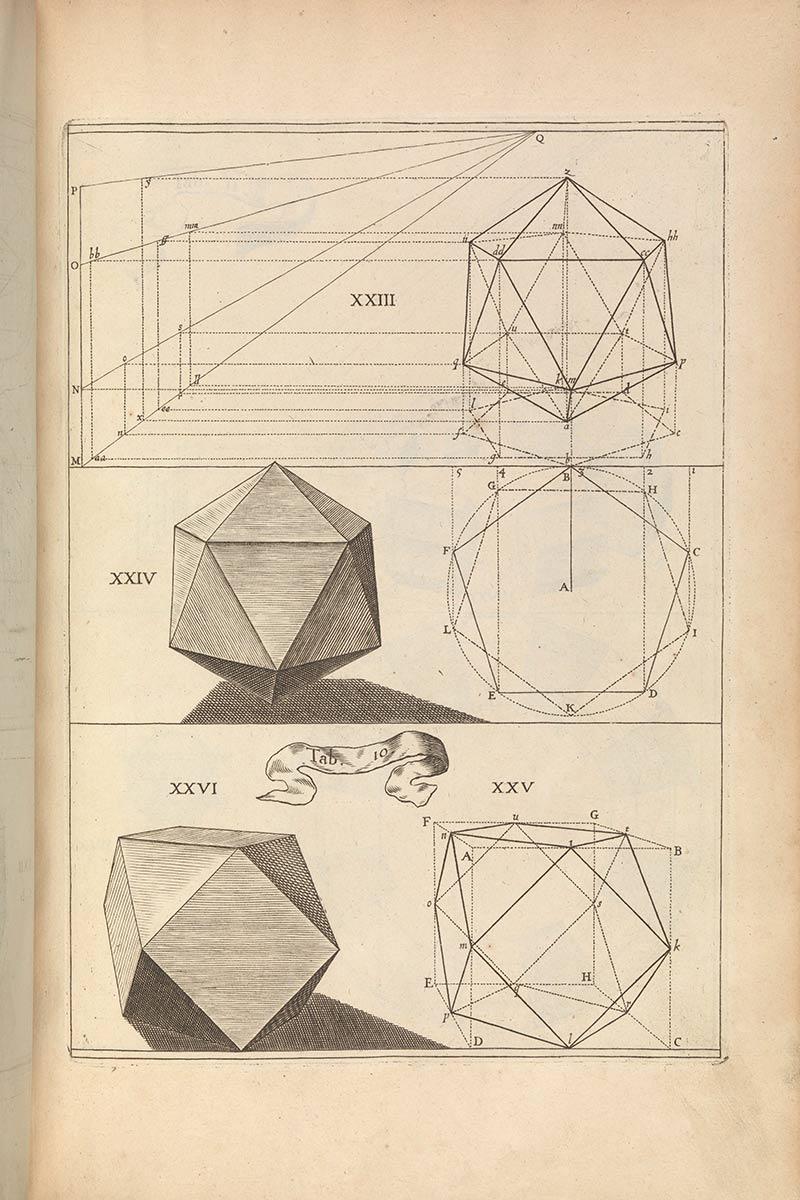
Escher was not the first printmaker to produce prints featuring regular polyhedra. In 1514, Albrecht Dürer produced the copper engraving Melencolia I, a print rich in symbolism, which is particularly evident in the contrast between the melancholic seated angel and the linear polyhedron to her left. A cube that raises plenty of questions due to two corners having been cut off. And it is not just the angel who is left to ponder these. Dürer was influenced by Pacioli and he went further by studying and depicting polyhedra. A next step in the study of polyhedra comes in the 1568 book Perspectiva corporum regularium by Wenzel Jamnitzer (1508-1585) and Jost Amman (1539-1591). It is brimming with perspective drawings and engravings of polyhedra, varying from basic shapes such as the tetrahedron or octahedron to all kinds of variants on these. The drawings were done by Jamnitzer and the engravings by Amman.

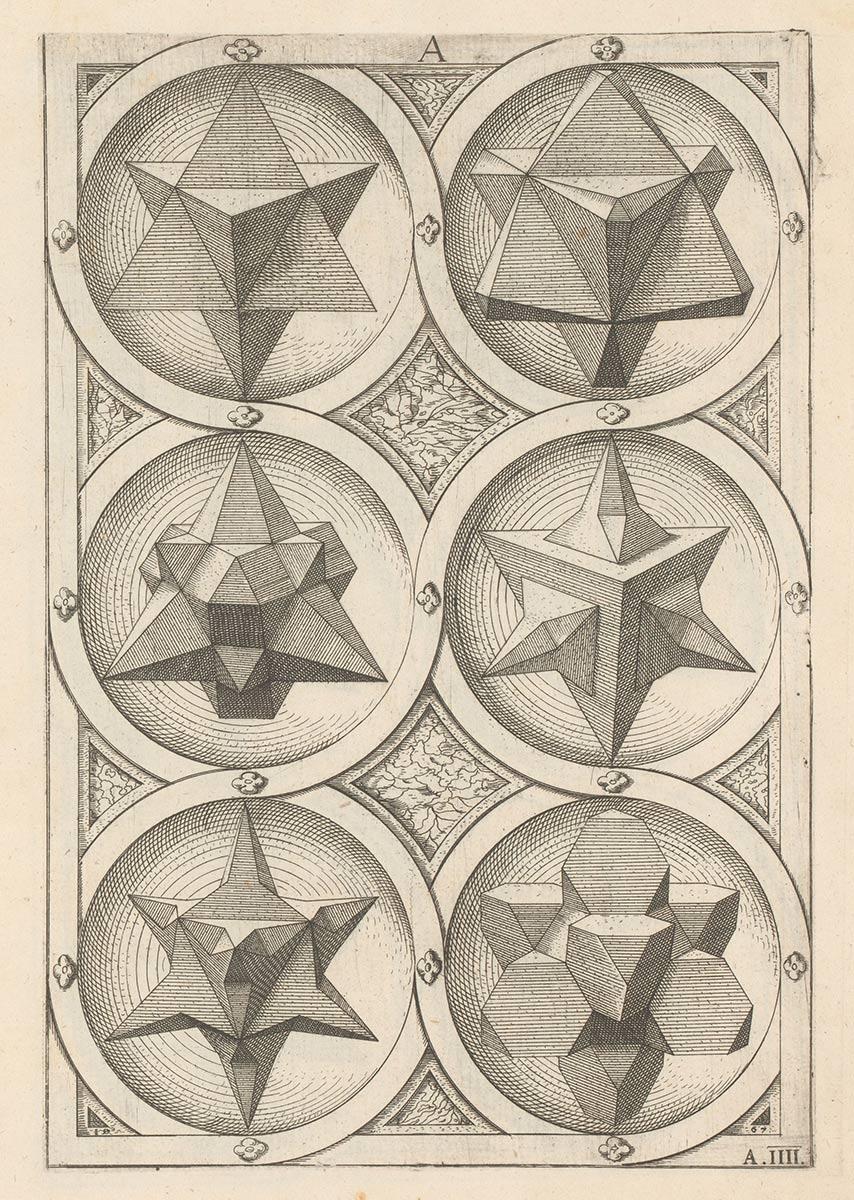
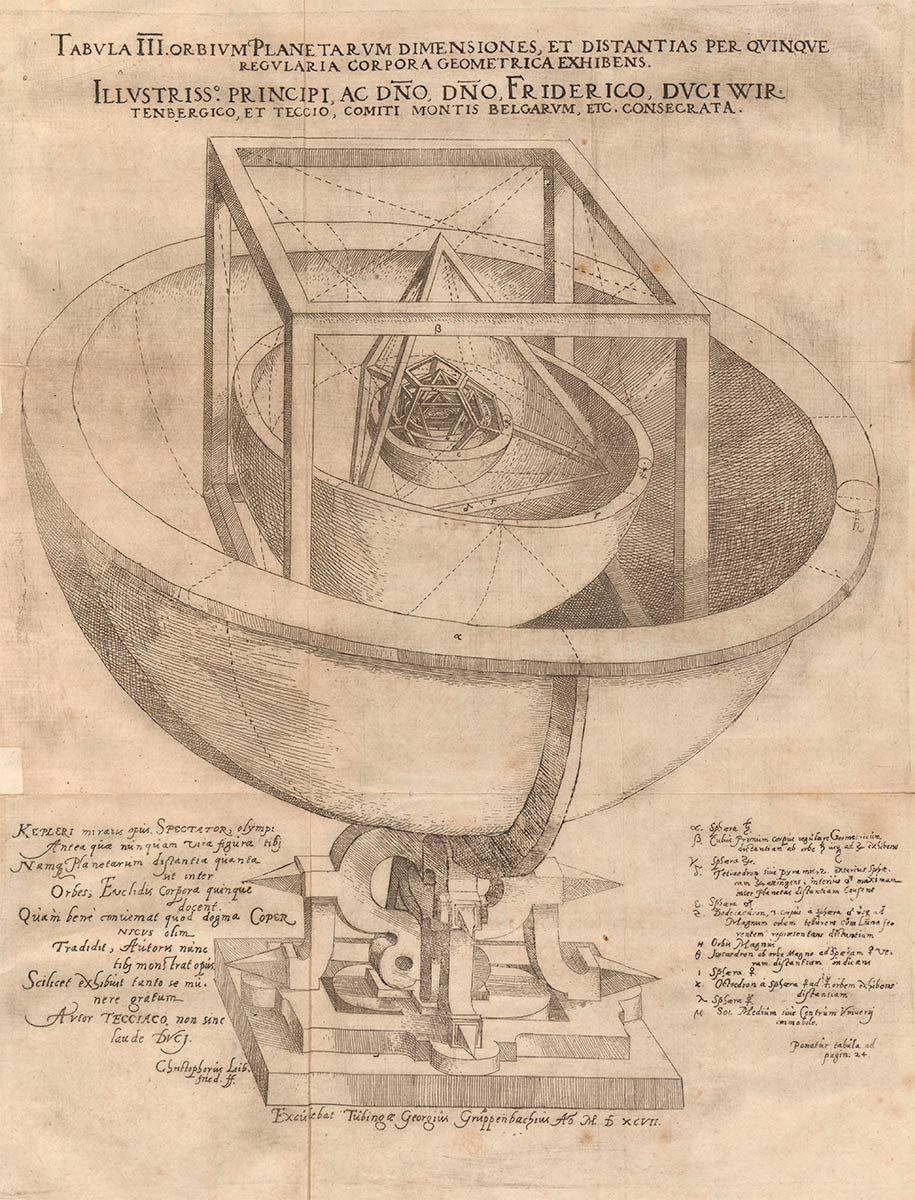
Kepler-Poinsot

In 1596, the German scientist Johannes Kepler (1571-1630) published the astronomy book Mysterium Cosmographicum. In it Kepler stated that the ratios of distance between the five planets known at the time could be understood in terms of the five Platonic solids enclosed in a sphere. His theory was corroborated once new planets were discovered, but the book once again attests to the extent of scientists’ fascination with these solids. His book Harmonices Mundi (1619) argues the case that everything in the universe is in harmony and that polyhedra and geometry play a significant role in that. Kepler also rediscovered the thirteen Archimedean solids and presented them in this book. In 1809, Louis Poinsot (1777-1859) rediscovered Kepler’s figures and came up with two new variants himself: the great icosahedron and the great dodecahedron. Nowadays the two scientists’ shapes are known as the Kepler-Poinsot (star) polyhedra. Other scientists who got involved with Platonic and Archimedean solids include Daniele Barbaro (1513-1570), Lorenz Stöer (c. 1540-1620), Simon Stevin (1548-1620), Jan Brożek (1585-1652), Jean-François Niçeron (1613-1646), Albert Badoureau (1853-1923) and H.S.M. Coxeter (1907-2003).

Escher’s fascination with regular polyhedra demonstrates that he was far from being a ‘normal’ artist. It is further proof of his unique status as a craftsman in the grey area between art and science. He sometimes felt misunderstood by both camps, but he was happy to sit at the intersection between the two. The perspex star dodecahedron currently on display at Escher in The Palace provides tangible evidence of Escher’s lifelong fascination with the tetrahedron, the hexahedron, the octahedron, the dodecahedron, the icosahedron and all those other polyhedra that attest to order and elegance in what is sometimes such a chaotic world.

Sources
* Visions of Symmetry: notebooks, periodic drawings, and related work of M.C. Escher, Doris Schattschneider, W.H. Freeman and Company, 1990, page 246-247
** and *** Letter to son George and his wife Corrie, 7 May 1961
For this article the following sources were also used:

• Historical Notes on Star Geometry in Mathematics, Art and Nature, by Aldo Brigaglia, Nicla Palladino and Maria Vaccaro, 2018
• Imagine Math 6: Between Culture and Mathematics edited by Michele Emmer and Marco Abate. Springer International Publishing, 2018
• Max Brückner’s Wunderkammer of Paper Polyhedra, by professor G.W. Hart, in Proceedings of Bridges, 2019