Magische veelvlakken

Het platte vlak was erg belangrijk voor M.C. Escher. Het tweedimensionale witte papier bood hem de mogelijkheid om het oneindige te onderzoeken en illusies op te wekken. Daarop creëerde Escher zijn driedimensionale werelden waarmee hij het oog van de kijker bedot. Werelden waarin orde en chaos met elkaar de strijd aan gaan, net als in de echte wereld. Maar waar die orde het in de echte wereld vaak verliest van de chaos, was het bij Escher andersom. Bij de uitreiking van de Hilversumse Cultuurprijs in 1965 zei hij er het volgende over:

‘Ik probeer in mijn prenten ervan te getuigen, dat wij leven in een schone, geordende wereld en niet in een normenloze chaos, zoals het soms lijkt.’

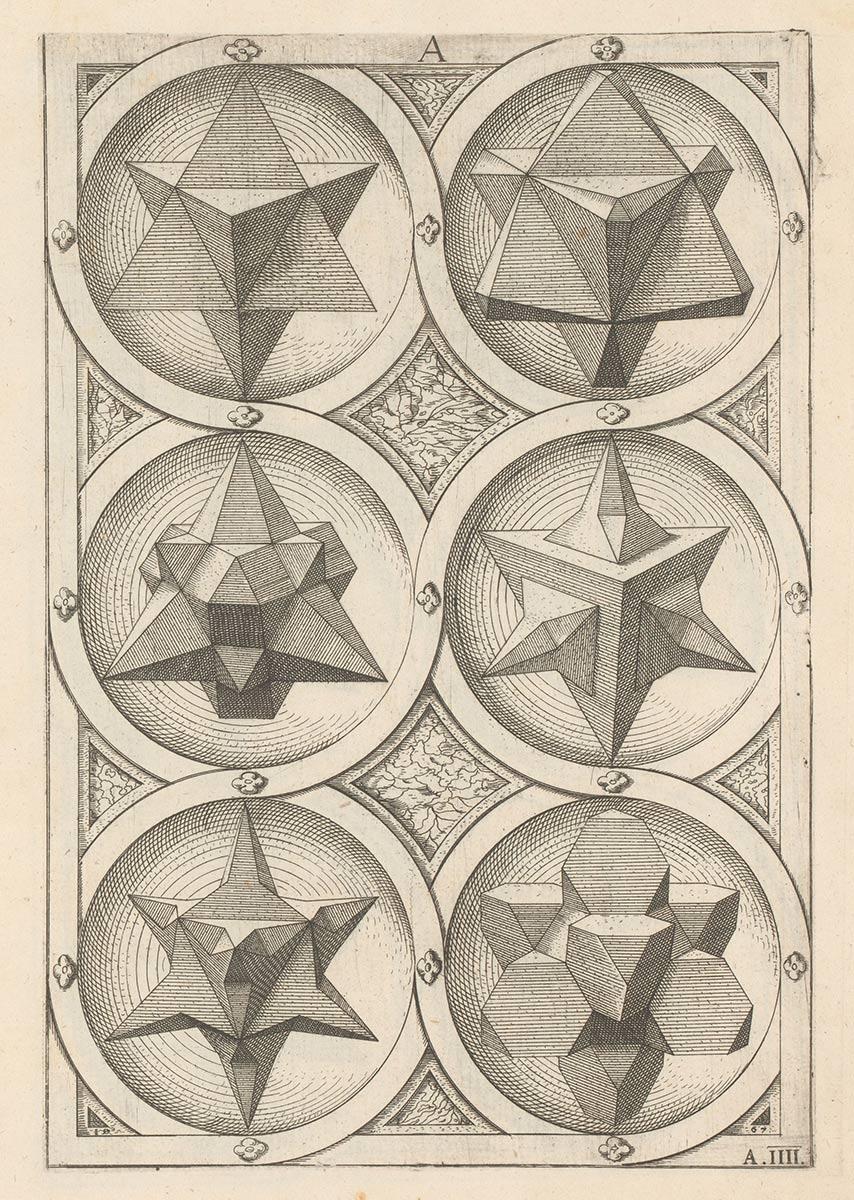
Als symbolen voor die orde gebruikte hij vaak regelmatige veelvlakken, de zogenaamde platonische en archimedische lichamen. Twee boeken werden een belangrijke inspiratiebron: Algemene mineralogie en kristallografie (1935), van zijn halfbroer Berend, en Vielecke und Vielflache: Theorie und Geschichte (1900) van Max Brückner (1860-1934)*. Dat laatste boek was vooral interessant omdat er talloze getekende afbeeldingen in stonden en ook 146 foto’s van papieren veelvlakmodellen uit de collectie van Brückner. Die afbeeldingen gebruikte Escher als bron voor zijn eigen tekeningen en modellen.

De platonische lichamen bestaan uit vijf soorten regelmatige veelvlakken, die voor het eerst zijn beschreven door de Griekse filosoof Plato (472-347 v. Chr.): de tetraëder, de hexaëder (of kubus), de octaëder, de dodecaëder en de icosaëder. De Griekse wiskundige Archimedes (287-212 v. Chr.) beschreef vervolgens de dertien archimedische lichamen, halfregelmatige veelvlakken die varianten zijn op de platonische lichamen. Escher toont een aantal van deze veelvlakken in zijn prenten, soms ook in aangepaste vorm. Het zijaanzicht van een kubus, met de drie tegen elkaar geschoven ruiten, duikt al op in Metamorphose I en Kringloop. In Reptielen is een dodecaëder te zien, in Kristal gebruikt hij een combinatie van kubus en octaëder en in Tegenstelling (Orde en chaos) en Zwaartekracht een sterdodecaëder, een twaalfvlak met op elk vlak een vijfhoekige piramide. In Vier regelmatige lichamen combineert hij zelfs vier van deze veelvlakken: een zes-, acht-, twaalf- en twintigvlak. Hij wilde er nog een tetraëder in kwijt, maar uiteindelijk besloot hij dat dit voor de toeschouwer te complex zou worden **.

Hoewel hij een grote liefde had voor het tweedimensionale in zijn prenten, week hij een enkele keer toch af naar het maken van een echte driedimensionale vorm. Soms was dat omdat hij zo’n wiskundig lichaam in een prent af wilde beelden en een model nodig had om het goed weer te kunnen geven. Het kon ook een autonome vorm zijn die als kunstwerk op zichzelf beschouwd kan worden.

Zo ontwierp hij voor blikfabrikant Verblifa een trommeltje in de vorm van een icosaëder, een twintigvlak. Die is in 1963 door de fabrikant in een oplage van 7000 gemaakt. Tien jaar daarvoor maakte Escher zelf een sterdodecaëder van perspex, in een oplage van twee. Het was een uitvoerig maakproces, wat Escher in 1953 in samenwerking met zijn zoon George, die studeerde aan de Technische Hogeschool in Delft, uitvoerde. Escher wilde het eerste exemplaar perfectioneren, dus hij heeft het project twee keer uitgevoerd. De individuele stukken perspex zijn door Escher gegutst met een patroon dat de de suggestie wekt van een zeester. George kreeg de taak om alle onderdelen met de hand aan elkaar te lijmen. Dit project moet een ware puzzel voor vader en zoon zijn geweest.

De perspex sterdodecaëder is nu te zien bij Escher in Het Paleis. Het is een bruikleen uit particulier bezit dat voor het eerst in een museum te bewonderen is.

Naar aanleiding van de prent Vier regelmatige lichamen schreef Escher ***:

‘Als je nou vraagt; waaróm doe je toch zulke gekheden, zulke absolute objectiviteiten die niets persoonlijks meer hebben? Dan kan ik alleen maar antwoorden: ik kan het niet laten. Dit geval is, bij mijn weten althans, nooit bevredigend opgelost door die groep van lui, omstreeks 15 en 1600, Dürer, Pacioli, Barbarbo en zelfs Leonardo. Zij hebben zich er ongetwijfeld oorspronkelijk op dezelfde wijze voor geïnteresseerd als ik: de schoonheid en de orde der regelmatige lichamen is overweldigend […]’

Lange traditie

Regelmatige, halfregelmatige en samengestelde veelvlakken hebben een lange geschiedenis in kunst en wetenschap. De Griekse wiskundige Euclides (ca. 325 v.C. – 256 v.C.) was de eerste die de door Plato gedefinieerde regelmatige vormen wiskundig beschreef in zijn verzamelwerk Elementen. Al uit de Romeinse tijd zijn fysieke dodecaëders bekend, maar hun functie is nog nooit opgehelderd. Veelvlakken belichamen niet alleen elegantie en wiskundige precisie, maar ze herbergen ook veel symboliek. Daarmee zijn ze interessant voor zowel wetenschappers als kunstenaars. Door de geschiedenis heen hebben beide groepen de lichamen bestudeerd en erover gepubliceerd of ze in hun kunst verwerkt. Het bekendste voorbeeld is Leonardo da Vinci (1452-1519), de Renaissancekunstenaar die zich op het snijvlak van kunst en wetenschap begaf en met wie Escher een grote verwantschap voelde. Da Vinci tekende de illustraties van regelmatige veelvlakken in het eerste deel van Divina proportione (1509) van Luca Pacioli (1445-1517). Op zijn beurt zou Escher de veelvlakken op een gelijksoortige opengewerkte manier afbeelden in zijn prent Sterren.

In hun fascinatie voor deze veelvlakken kregen Da Vinci en Pacioli gezelschap van kunstenaar-wetenschappers als Piero della Francesca (ca. 1415-1492) en Albrecht Dürer (1471-1528). Allen hadden zich echter altijd te verhouden tot religie, omdat wetenschappers vaak ook geestelijken waren. De kerk was een machtige opdrachtgever en soms ook tegenstander. Een van de vroegste voorbeelden van opdrachtgeverschap is de kleine sterdodecaëder die te zien is in een vloermozaïek (c. 1425) in de Basiliek van San Marco in Venetië. Het mozaïek wordt toegeschreven aan Paolo Uccello (1397-1475). In de late Renaissance en de eeuwen daarna verschenen er op obelisken en kerkgebouwen in Europa stervormige veelvlakken, als symbool voor God en de kerk.
Escher was niet de eerste graficus die prenten maakte met regelmatige veelvlakken. In 1514 maakte Albrecht Dürer de kopergravure Melencolia I, een prent vol symboliek die vooral opvalt door het contrast tussen de melancholische zittende engel en het strakke veelvlak aan de linkerkant. Een kubus die door de twee afgesneden hoeken veel vragen oproept. Niet alleen bij de engel. Dürer was beïnvloed door Pacioli en hij ging verder met het onderzoeken en afbeelden van veelvlakken. Een volgende stap in dat onderzoek is het in 1568 verschenen boek Perspectiva corporum regularium van Wenzel Jamnitzer (1507/1508-1585) en Jost Amman (1539-1591). Het is gevuld met talloze perspectieftekeningen en gravures van veelvlakken, variërend van basisvormen als de tetraëder of octaëder tot allerlei varianten daarop. De tekeningen waren gemaakt door Jamnitzer en de gravures door Amman.

Kepler-Poinsot

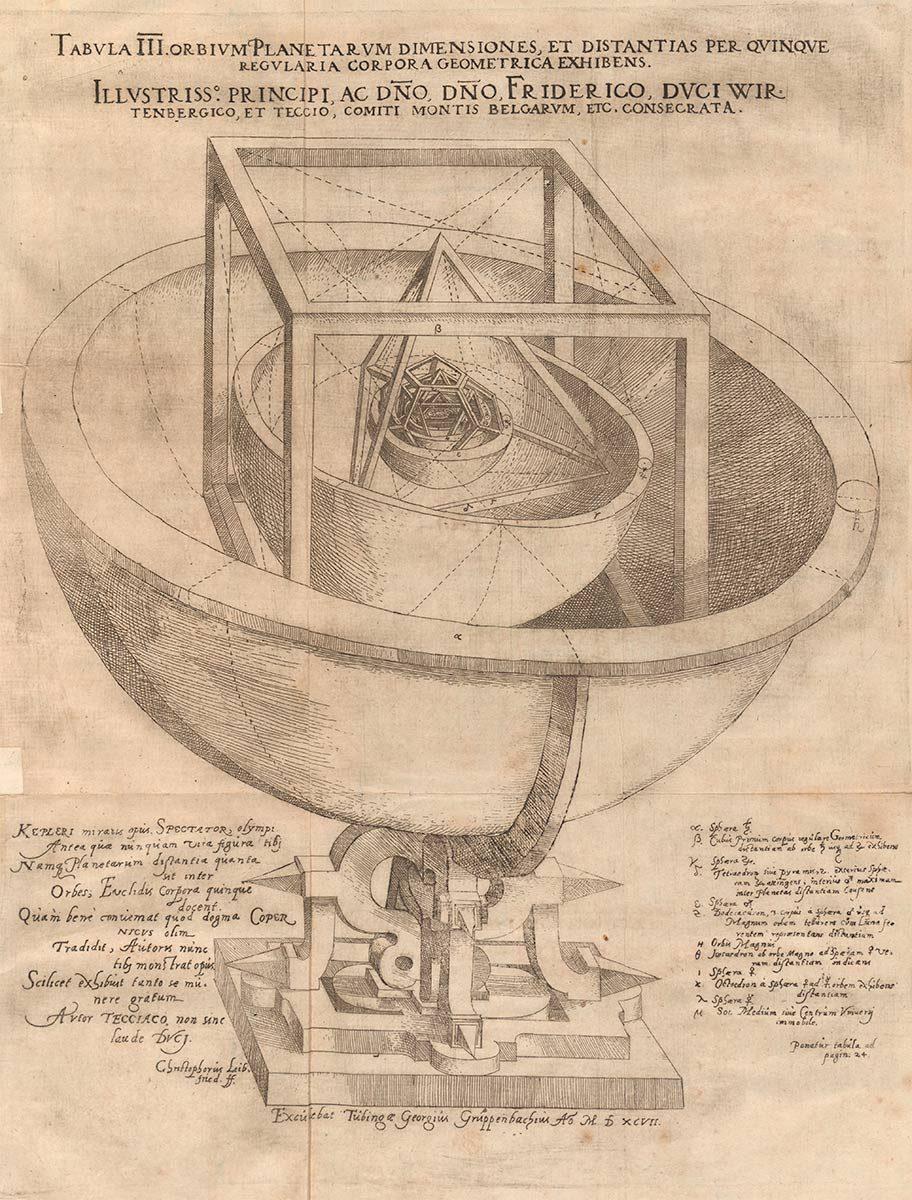
In 1596 publiceerde de Duitse wetenschapper Johannes Kepler (1571-1630) het astronomisch boek Mysterium Cosmographicum. Kepler stelde daarin dat de afstandsverhoudingen tussen de vijf toen bekende planeten konden worden begrepen in termen van de vijf platonische lichamen, ingesloten in een bol. Toen er nieuwe planeten ontdekt werden, bleek die theorie achterhaald, maar het boek laat nogmaals zien hoezeer wetenschappers gefascineerd waren door deze lichamen. Zijn boek Harmonices Mundi (1619) is een pleidooi voor de stelling dat alles in de kosmos in harmonie is met elkaar en dat veelvlakken en geometrie daarin een grote rol spelen. Kepler herontdekte ook de dertien archimedische lichamen en in dit boek zijn ze allemaal te zien. In 1809 herontdekte Louis Poinsot (1777-1859) de figuren van Kepler en hij kwam zelf tot twee nieuwe varianten: de grote icosaëder en de grote dodecaëder. Tegenwoordig staan de vormen van de twee wetenschappers bekend als de Kepler-Poinsot (stervormige) veelvlakken. Andere wetenschappers die zich bezighielden met platonische en archimedische lichamen waren Daniele Barbaro (1514-1570), Lorenz Stöer (c. 1540-1620), Simon Stevin (1548-1620), Jan Brożek (1585-1652), Jean-François Niçeron (1613-1646), Albert Badoureau (1853-1923) en H.S.M. Coxeter (1907-2003).

Met zijn fascinatie voor regelmatige veelvlakken toont Escher aan dat hij zeker geen ‘gewone’ kunstenaar was. Het is eens te meer een illustratie van zijn unieke positie als een ambachtsman die in het schemergebied staat tussen kunst en wetenschap. Door beide kampen voelde hij zich soms onbegrepen, maar hij was ook blij met deze plek. De perspex sterdodecaëder die nu te zien is bij Escher in Het Paleis vormt een tastbaar bewijs van Eschers levenslange fascinatie voor de tetraëder, de hexaëder, de octaëder, de dodecaëder, de icosaëder en al die andere veelvlakken die getuigen van orde en elegantie in een soms zo chaotische wereld.

Bronnen
* Visions of Symmetry: notebooks, periodic drawings, and related work of M.C. Escher, Doris Schattschneider, W.H. Freeman and Company, 1990, blz. 246-247.
** en *** Brief aan zoon George en diens vrouw Corrie, 7 mei 1961
Voor dit artikel zijn ook de volgende bronnen gebruikt:

• Historical Notes on Star Geometry in Mathematics, Art and Nature, door Aldo Brigaglia, Nicla Palladino en Maria Vaccaro, 2018
• Imagine Math 6: Between Culture and Mathematics geredigeerd door Michele Emmer en Marco Abate. Springer International Publishing, 2018
• Max Brückner’s Wunderkammer of Paper Polyhedra, door professor G.W. Hart, in Proceedings of Bridges, 2019